Every thing you need to know about Linked List
A linked list is a linear data structure, in which the elements are not stored at contiguous memory locations. The elements in a linked list are linked using pointers as shown in the below image:
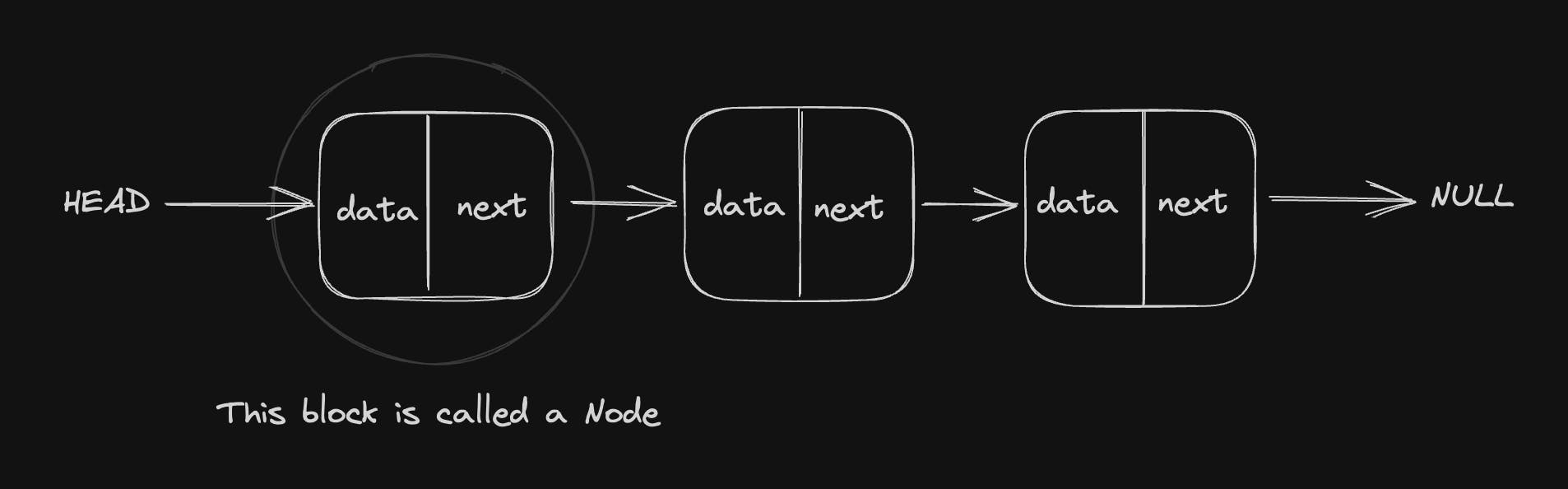
In simple we can say that a linked list forms a series of connected nodes, where each node has a data field and reference of the next data field in the sequence that is stored in the next field.
A linked list is assessed through the first node of the list known as the Head Node. The last node in the list points to NULL or nullptr, which indicates the end of the list this node is known as the Tail node.
In the above diagram, I have used the structure of a Single-Linked List. Apart from a Single-linked List, there are more two types of linked lists namely Double-Linked List and Circular Linked List, I will cover all the types and their structure in brief in the later part of this article.
Now you might be thinking that it is similar to an Array, then why use it instead of an Array?
Let's find out, why.
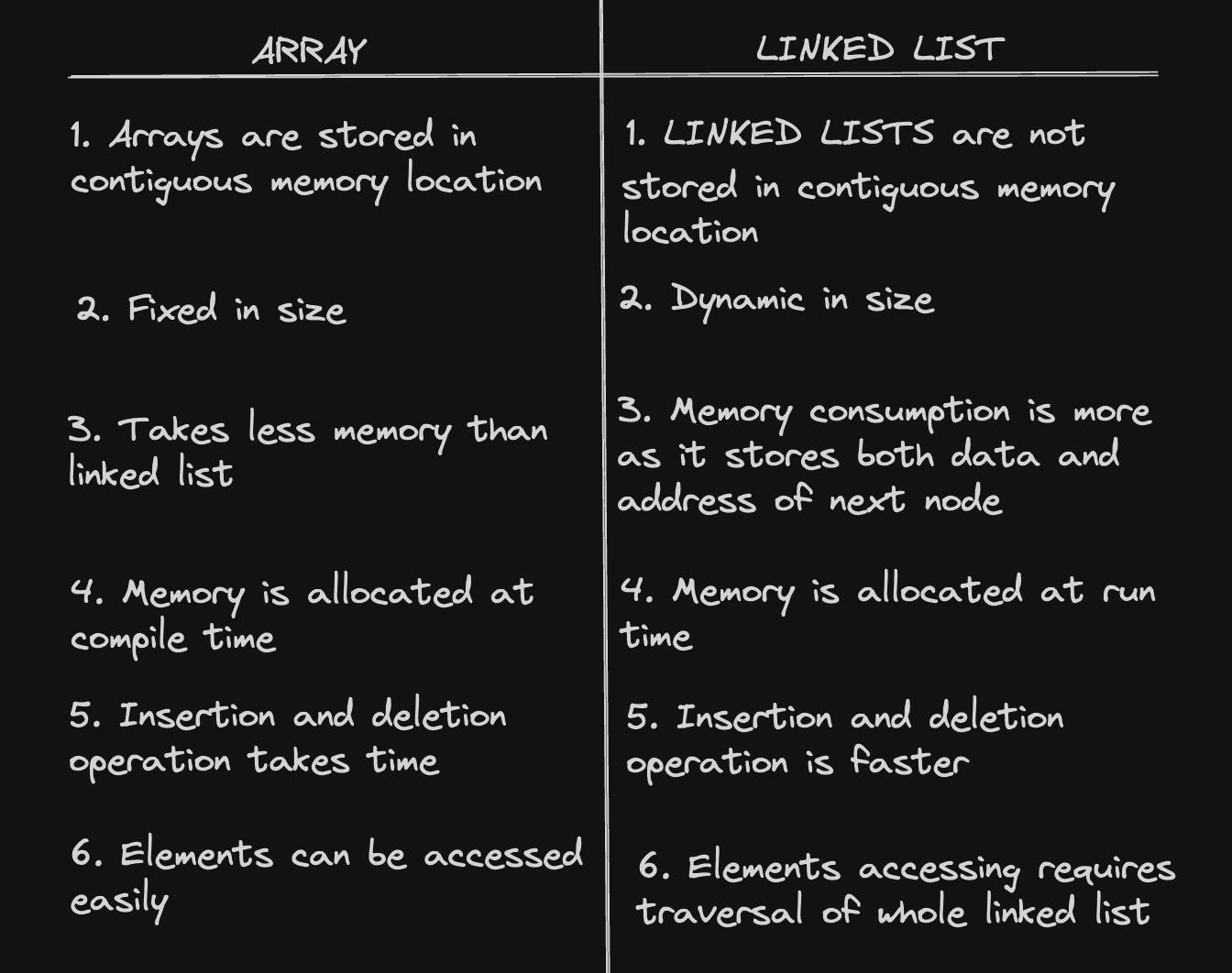
Arrays store data in contiguous memory locations, which allows faster access to an element at a specific index. On the other hand, Linked Lists are less rigid in their storage structure and elements are usually not stored in contiguous locations, hence they need to be stored with additional tags giving a reference to the next element.
Based on the above information we can conclude that Linked Lists are like flexible containers that can change their size easily. They're great when you want to add or remove things without knowing how many you'll have ahead of time. Adding or removing stuff from the middle of a linked list is quick and doesn't mess up the rest. But if you need to find something in a hurry, linked lists might not be as fast as arrays, which are like neatly lined-up boxes where you can grab something instantly. So, use linked lists when you want flexibility and easy changes, but consider arrays when you need fast access to items.
The major difference between these two is as follows:
Advantages of Linked List:
Linked lists are a popular data structure in computer science, and have several advantages over other data structures, such as arrays. Some of the key advantages of linked lists are:
Dynamic size: Linked lists do not have a fixed size, so you can add or remove elements as needed, without having to worry about the size of the list. This makes linked lists a great choice when you need to work with a collection of items whose size can change dynamically.
Efficient Insertion and Deletion: Inserting or deleting elements in a linked list is fast and efficient, as you only need to modify the reference of the next node, which is an O(1) operation.
Memory Efficiency: Linked lists use only as much memory as they need, so they are more efficient with memory compared to arrays, which have a fixed size and can waste memory if not all elements are used.
Easy to Implement: Linked lists are relatively simple to implement and understand compared to other data structures like trees and graphs.
Flexibility: Linked lists can be used to implement various abstract data types, such as stacks, queues, and associative arrays.
Easy to navigate: Linked lists can be easily traversed, making it easier to find specific elements or perform operations on the list.
In conclusion, linked lists are a powerful and flexible data structure that has several advantages over other data structures, making them a great choice for solving many data structure and algorithm problems.
Disadvantages of Linked List:
Linked lists are a popular data structure in computer science, but like any other data structure, they have certain disadvantages as well. Some of the key disadvantages of linked lists are:
Slow Access Time: Accessing elements in a linked list can be slow, as you need to traverse the linked list to find the element you are looking for, which is an O(n) operation. This makes linked lists a poor choice for situations where you need to access elements quickly.
Pointers: Linked lists use pointers to reference the next node, which can make them more complex to understand and use compared to arrays. This complexity can make linked lists more difficult to debug and maintain.
Higher overhead: Linked lists have a higher overhead compared to arrays, as each node in a linked list requires extra memory to store the reference to the next node.
Cache Inefficiency: Linked lists are cache-inefficient because the memory is not contiguous. This means that when you traverse a linked list, you are not likely to get the data you need in the cache, leading to cache misses and slow performance.
Extra memory required: Linked lists require an extra pointer for each node, which takes up extra memory. This can be a problem when you are working with large data sets, as the extra memory required for the pointers can quickly add up.
Some applications of Linked list are listed below:
Linked Lists are used to implement stacks and queues.
It is used for the various representations of trees and graphs.
It is used in dynamic memory allocation( linked list of free blocks).
It is used for representing sparse matrices.
It is used for the manipulation of polynomials.
It is also used for performing arithmetic operations on long integers.
It is used for finding paths in networks.
In operating systems, they can be used in Memory management, process scheduling and file systems.
Linked lists can be used to improve the performance of algorithms that need to frequently insert or delete items from large collections of data.
Implementing algorithms such as the LRU cache, which uses a linked list to keep track of the most recently used items in a cache.
The list of songs in the music player is linked to the previous and next songs.
In a web browser, previous and next web page URLs are linked through the previous and next buttons.
In the image viewer, the previous and next images are linked with the help of the previous and next buttons.
Switching between two applications is carried out by using “alt+tab” in Windows and “cmd+tab” in mac book. It requires the functionality of a circular linked list.
On mobile phones, we save the contacts of people. The newly entered contact details will be placed in the correct alphabetical order. This can be achieved by a linked list to set contact at the correct alphabetical position.
The modifications that we make in documents are created as nodes in the doubly linked list. We can simply use the undo option by pressing Ctrl+Z to modify the contents. It is done by the functionality of a linked list.
Now let us continue with the types of Linked Lists.
As I mentioned earlier there are three types of Linked Lists, well it has other variations as well, these are listed below:
Singly Linked List:
It is the simplest type of linked list in which every node contains some data and a pointer to the next node of the same data type.
The node contains a pointer to the next node means that the node stores the address of the next node in the sequence. A single linked list allows the traversal of data only in one way. Below is the image for the same:
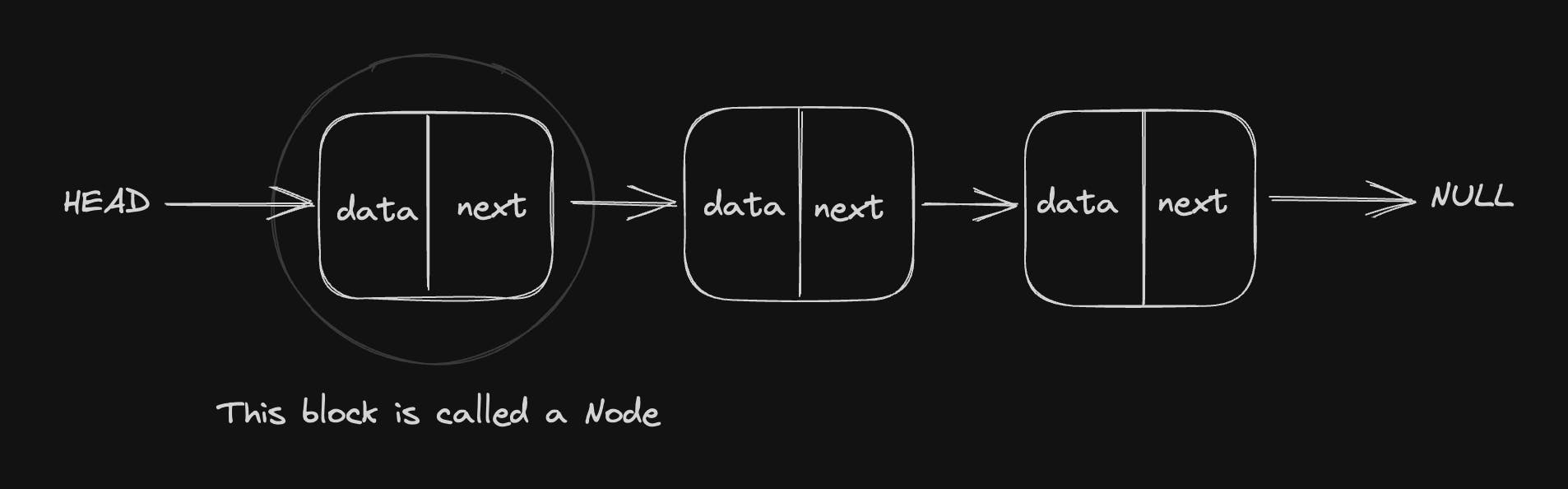
Below is the structure of a singly linked list in C++
// Node of a singly linked list
class Node {
public:
int data;
// Pointer to next node in LL
Node* next;
};
// C++ program to illustrate creation
// and traversal of Singly Linked List
#include <bits/stdc++.h>
using namespace std;
// Structure of Node
class Node {
public:
int data;
Node* next;
};
// Function to print the content of
// linked list starting from the
// given node
void printList(Node* n)
{
// Iterate till n reaches NULL
while (n != NULL) {
// Print the data
cout << n->data << " ";
n = n->next;
}
}
// Driver Code
int main()
{
Node* head = NULL;
Node* second = NULL;
Node* third = NULL;
// Allocate 3 nodes in the heap
head = new Node();
second = new Node();
third = new Node();
// Assign data in first node
head->data = 1;
// Link first node with second
head->next = second;
// Assign data to second node
second->data = 2;
second->next = third;
// Assign data to third node
third->data = 3;
third->next = NULL;
printList(head);
return 0;
}
Output
1 2 3
Time Complexity: O(N)
Characteristics of a Singly Linked List:
Each node holds a single value and a reference to the next node in the list.
The list has a head, which is a reference to the first node in the list, and a tail, which is a reference to the last node in the list.
The nodes are not stored in a contiguous block of memory, but instead, each node holds the address of the next node in the list.
Accessing elements in a singly linked list requires traversing the list from the head to the desired node, as there is no direct access to a specific node in memory.
Application of Singly Linked Lists:
Memory management: Singly linked lists can be used to implement memory pools, in which memory is allocated and deallocated as needed.
Database indexing: Singly linked lists can be used to implement linked lists in databases, allowing for fast insertion and deletion operations.
Representing polynomials and sparse matrices: Singly linked lists can be used to efficiently represent polynomials and sparse matrices, where most elements are zero.
Operating systems: Singly linked lists are used in operating systems for tasks such as scheduling processes and managing system resources.
Advantages of Singly Linked Lists:
Dynamic memory allocation: Singly linked lists allow for dynamic memory allocation, meaning that the size of the list can change at runtime as elements are added or removed.
Cache friendliness: Singly linked lists can be cache-friendly as nodes can be stored in separate cache lines, reducing cache misses and improving performance.
Space-efficient: Singly linked lists are space-efficient, as they only need to store a reference to the next node in each element, rather than a large block of contiguous memory.
Disadvantages of Singly Linked Lists:
Poor random access performance: Accessing an element in a singly linked list requires traversing the list from the head to the desired node, making it slow for random access operations compared to arrays.
Increased memory overhead: Singly linked lists require additional memory for storing the pointers to the next node in each element, resulting in increased memory overhead compared to arrays.
Vulnerability to data loss: Singly linked lists are vulnerable to data loss if a node’s next pointer is lost or corrupted, as there is no way to traverse the list and access other elements.
Not suitable for parallel processing: Singly linked lists are not suitable for parallel processing, as updating a node requires exclusive access to its next pointer, which cannot be easily done in a parallel environment.
Backward traversing not possible: In singly linked list does not support backward traversing.
Doubly Linked List
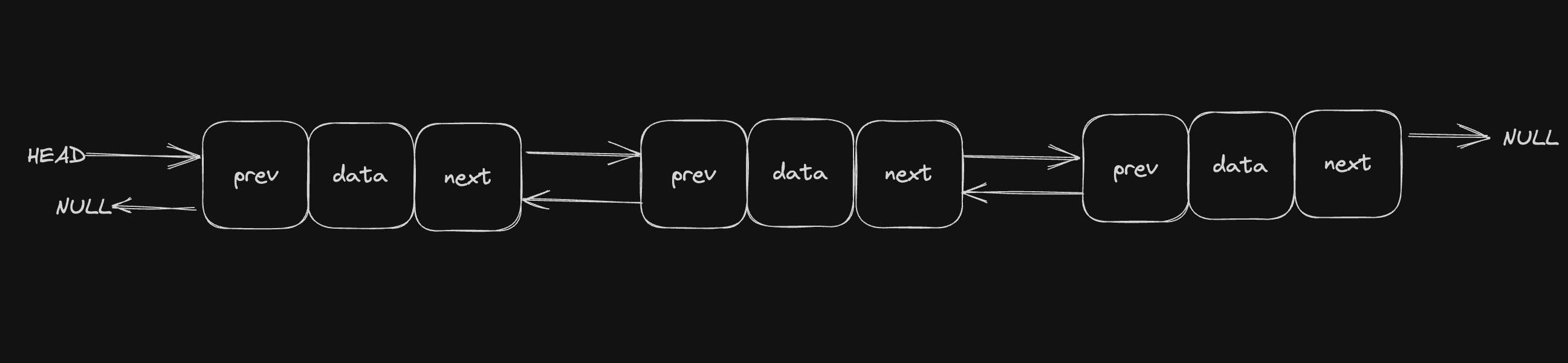
A doubly linked list or a two-way linked list is a more complex type of linked list that contains a pointer to the next as well as the previous node in the sequence.
Therefore, it contains three parts of data, a pointer to the next node, and a pointer to the previous node. This would enable us to traverse the list in the backward direction as well. Below is the image for the same:
// Node of a doubly linked list
struct Node {
int data;
// Pointer to next node in DLL
struct Node* next;
// Pointer to the previous node in DLL
struct Node* prev;
};
// C++ program to illustrate creation
// and traversal of Doubly Linked List
#include <bits/stdc++.h>
using namespace std;
// Doubly linked list node
class Node {
public:
int data;
Node* next;
Node* prev;
};
// Function to push a new element in
// the Doubly Linked List
void push(Node** head_ref, int new_data)
{
// Allocate node
Node* new_node = new Node();
// Put in the data
new_node->data = new_data;
// Make next of new node as
// head and previous as NULL
new_node->next = (*head_ref);
new_node->prev = NULL;
// Change prev of head node to
// the new node
if ((*head_ref) != NULL)
(*head_ref)->prev = new_node;
// Move the head to point to
// the new node
(*head_ref) = new_node;
}
// Function to traverse the Doubly LL
// in the forward & backward direction
void printList(Node* node)
{
Node* last;
cout << "\nTraversal in forward"
<< " direction \n";
while (node != NULL) {
// Print the data
cout << " " << node->data << " ";
last = node;
node = node->next;
}
cout << "\nTraversal in reverse"
<< " direction \n";
while (last != NULL) {
// Print the data
cout << " " << last->data << " ";
last = last->prev;
}
}
// Driver Code
int main()
{
// Start with the empty list
Node* head = NULL;
// Insert 6.
// So linked list becomes 6->NULL
push(&head, 6);
// Insert 7 at the beginning. So
// linked list becomes 7->6->NULL
push(&head, 7);
// Insert 1 at the beginning. So
// linked list becomes 1->7->6->NULL
push(&head, 1);
cout << "Created DLL is: ";
printList(head);
return 0;
}
Output
Created DLL is:
Traversal in forward direction
1 7 6
Traversal in reverse direction
6 7 1
Time Complexity:
The time complexity of the push() function is O(1) as it performs constant-time operations to insert a new node at the beginning of the doubly linked list. The time complexity of the printList() function is O(n) where n is the number of nodes in the doubly linked list. This is because it traverses the entire list twice, once in the forward direction and once in the backward direction. Therefore, the overall time complexity of the program is O(n).
Applications of Doubly Linked List:
It is used by web browsers for backward and forward navigation of web pages
LRU ( Least Recently Used ) / MRU ( Most Recently Used ) Cache are constructed using Doubly Linked Lists.
Used by various applications to maintain undo and redo functionalities.
In Operating Systems, a doubly linked list is maintained by thread scheduler to keep track of processes that are being executed at that time.
Advantages of Doubly Linked List over the singly linked list:
A DLL can be traversed in both forward and backward directions.
The delete operation in DLL is more efficient if a pointer to the node to be deleted is given.
We can quickly insert a new node before a given node.
In a singly linked list, to delete a node, a pointer to the previous node is needed. To get this previous node, sometimes the list is traversed. In DLL, we can get the previous node using the previous pointer.
Disadvantages of Doubly Linked List over the singly linked list:
Every node of DLL Requires extra space for a previous pointer. It is possible to implement DLL with a single pointer though.
All operations require an extra pointer previous to be maintained. For example, in insertion, we need to modify previous pointers together with the next pointers.
Circular Linked List:
A circular linked list is that in which the last node contains the pointer to the first node of the list.
While traversing a circular linked list, we can begin at any node and traverse the list in any direction forward and backward until we reach the same node we started. Thus, a circular linked list has no beginning and no end. Below is the image for the same:
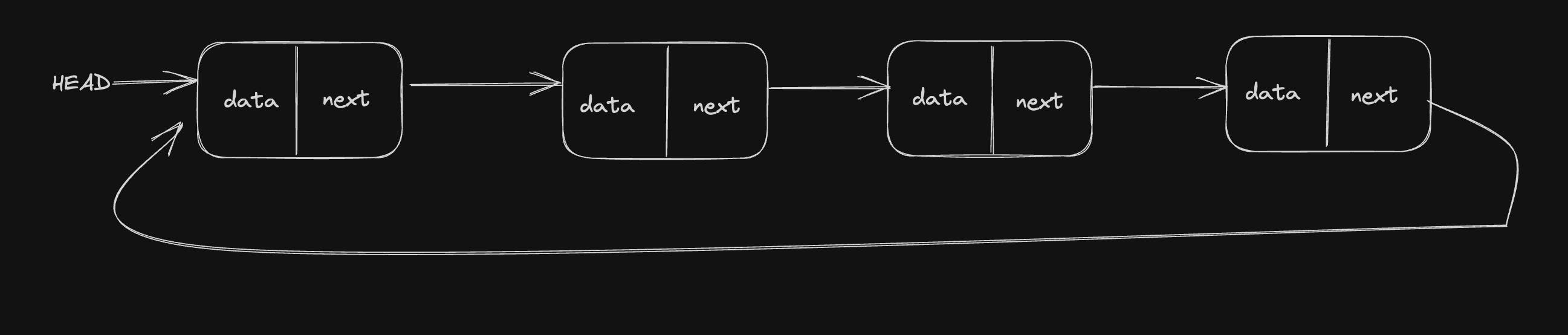
Below is the structure of the Circular Linked List:
// Structure for a node
class Node {
public:
int data;
// Pointer to next node in CLL
Node* next;
};
// C++ program to illustrate creation
// and traversal of Circular LL
#include <bits/stdc++.h>
using namespace std;
// Structure for a node
class Node {
public:
int data;
Node* next;
};
// Function to insert a node at the
// beginning of Circular LL
void push(Node** head_ref, int data)
{
Node* ptr1 = new Node();
Node* temp = *head_ref;
ptr1->data = data;
ptr1->next = *head_ref;
// If linked list is not NULL then
// set the next of last node
if (*head_ref != NULL) {
while (temp->next != *head_ref) {
temp = temp->next;
}
temp->next = ptr1;
}
// For the first node
else
ptr1->next = ptr1;
*head_ref = ptr1;
}
// Function to print nodes in the
// Circular Linked List
void printList(Node* head)
{
Node* temp = head;
if (head != NULL) {
do {
// Print the data
cout << temp->data << " ";
temp = temp->next;
} while (temp != head);
}
}
// Driver Code
int main()
{
// Initialize list as empty
Node* head = NULL;
// Created linked list will
// be 11->2->56->12
push(&head, 12);
push(&head, 56);
push(&head, 2);
push(&head, 11);
cout << "Contents of Circular"
<< " Linked List\n ";
// Function call
printList(head);
return 0;
}
Output
Contents of Circular Linked List
11 2 56 12
Time Complexity:
Insertion at the beginning of the circular linked list takes O(1) time complexity.
Traversing and printing all nodes in the circular linked list takes O(n) time complexity where n is the number of nodes in the linked list.
Therefore, the overall time complexity of the program is O(n).
Applications of circular linked lists:
Multiplayer games use this to give each player a chance to play.
A circular linked list can be used to organize multiple running applications on an operating system. These applications are iterated over by the OS.
Circular linked lists can be used in resource allocation problems.
Circular linked lists are commonly used to implement circular buffers,
Circular linked lists can be used in simulation and gaming.
**
Advantages of Circular Linked Lists:**
Any node can be a starting point. We can traverse the whole list by starting from any point. We just need to stop when the first visited node is visited again.
Useful for implementation of a queue.
Circular lists are useful in applications to repeatedly go around the list. For example, when multiple applications are running on a PC, it is common for the operating system to put the running applications on a list and then cycle through them, giving each of them a slice of time to execute, and then making them wait while the CPU is given to another application. It is convenient for the operating system to use a circular list so that when it reaches the end of the list it can cycle around to the front of the list.
Circular Doubly Linked Lists are used for the implementation of advanced data structures like the Fibonacci Heap.
Implementing a circular linked list can be relatively easy compared to other more complex data structures like trees or graphs.
Disadvantages of circular linked list:
Compared to singly linked lists, circular lists are more complex.
Reversing a circular list is more complicated than singly or doubly reversing a circular list.
It is possible for the code to go into an infinite loop if it is not handled carefully.
It is harder to find the end of the list and control the loop.
Although circular linked lists can be efficient in certain applications, their performance can be slower than other data structures in certain cases, such as when the list needs to be sorted or searched.
Circular linked lists don’t provide direct access to individual nodes
Doubly Circular linked list
A Doubly Circular linked list or a circular two-way linked list is a more complex type of linked list that contains a pointer to the next as well as the previous node in the sequence. The difference between the doubly linked and circular doubly list is the same as that between a singly linked list and a circular linked list. The circular doubly linked list does not contain null in the previous field of the first node. Below is the image for the same:

Below is the structure of the Doubly Circular Linked List:
// Node of doubly circular linked list
struct Node {
int data;
// Pointer to next node in DCLL
struct Node* next;
// Pointer to the previous node in DCLL
struct Node* prev;
};
// C++ program to illustrate creation
// & traversal of Doubly Circular LL
#include <bits/stdc++.h>
using namespace std;
// Structure of a Node
struct Node {
int data;
struct Node* next;
struct Node* prev;
};
// Function to insert Node at
// the beginning of the List
void insertBegin(struct Node** start, int value)
{
// If the list is empty
if (*start == NULL) {
struct Node* new_node = new Node;
new_node->data = value;
new_node->next = new_node->prev = new_node;
*start = new_node;
return;
}
// Pointer points to last Node
struct Node* last = (*start)->prev;
struct Node* new_node = new Node;
// Inserting the data
new_node->data = value;
// Update the previous and
// next of new node
new_node->next = *start;
new_node->prev = last;
// Update next and previous
// pointers of start & last
last->next = (*start)->prev = new_node;
// Update start pointer
*start = new_node;
}
// Function to traverse the circular
// doubly linked list
void display(struct Node* start)
{
struct Node* temp = start;
printf("\nTraversal in"
" forward direction \n");
while (temp->next != start) {
printf("%d ", temp->data);
temp = temp->next;
}
printf("%d ", temp->data);
printf("\nTraversal in "
"reverse direction \n");
Node* last = start->prev;
temp = last;
while (temp->prev != last) {
// Print the data
printf("%d ", temp->data);
temp = temp->prev;
}
printf("%d ", temp->data);
}
// Driver Code
int main()
{
// Start with the empty list
struct Node* start = NULL;
// Insert 5
// So linked list becomes 5->NULL
insertBegin(&start, 5);
// Insert 4 at the beginning
// So linked list becomes 4->5
insertBegin(&start, 4);
// Insert 7 at the end
// So linked list becomes 7->4->5
insertBegin(&start, 7);
printf("Created circular doubly"
" linked list is: ");
display(start);
return 0;
}
Output
Created circular doubly linked list is:
Traversal in forward direction
7 4 5
Traversal in reverse direction
5 4 7
Time Complexity:
Insertion at the beginning of a doubly circular linked list takes O(1) time complexity.
Traversing the entire doubly circular linked list takes O(n) time complexity, where n is the number of nodes in the linked list.
Therefore, the overall time complexity of the program is O(n).
Applications of Circular Doubly Linked List :
Circular doubly linked lists are used in a variety of applications, some of which include:
Implementation of Circular Data Structures: Circular doubly linked lists are extremely helpful in the construction of circular data structures like circular queues and circular buffers, which are both circular in nature.
Implementing Undo-Redo Operations: Text editors and other software programs can use circular doubly linked lists to implement undo-redo operations.
Music Player Playlist: Playlists in music players are frequently implemented using circular doubly linked lists. Each song is kept as a node in the list in this scenario, and the list can be circled to play the songs in the order they are listed.
Cache Memory Management: To maintain track of the most recently used cache blocks, circular doubly linked lists are employed in cache memory management.
Advantages of Circular Doubly Linked List:
Efficient traversal: Circular doubly linked lists allow efficient traversal in both forward and backward directions. This makes them useful for applications where bidirectional traversal is required, such as in music playlists or video players.
Constant time insertion and deletion: Insertion and deletion operations can be performed in constant time at any position in the list, unlike singly linked lists which require traversing the list to find the previous node before insertion or deletion.
More efficient memory allocation: In a circular doubly linked list, each node contains pointers to both the next and previous nodes, as well as the data element. This means that only a single memory allocation is required for each node, rather than two separate allocations required by singly linked lists.
Useful for implementing data structures: Circular doubly linked lists are useful for implementing other data structures, such as queues, deques, and hash tables. They also provide a good foundation for implementing algorithms such as graph traversal and sorting.
Can be used for circular data structures: Circular doubly linked lists are well-suited for circular data structures, where the last element is connected to the first element. Examples of circular data structures include circular buffers and circular queues.
Disadvantages of Circular Doubly Linked List:
More complex implementation: Implementing circular doubly linked lists is more complex than implementing other types of linked lists. This is because each node has to maintain pointers to both the next and previous nodes, as well as handle circularity properly.
More memory overhead: Each node in a circular doubly linked list contains pointers to both the next and previous nodes, which requires more memory overhead compared to singly linked lists.
More difficult to debug: Circular doubly linked lists can be more difficult to debug than other types of linked lists. This is because they have more complex pointer relationships and circularity, which can make it harder to trace errors and debug issues.
Not suitable for all applications: While circular doubly linked lists are useful for many applications, they may not be the best choice for all scenarios. For example, if bidirectional traversal is not required, a singly linked list may be a better choice. Additionally, if memory usage is a concern, a dynamic array or other data structure may be more efficient.
Extra care is needed when modifying the list: Modifying a circular doubly linked list requires extra care to ensure that the circularity is maintained. If the circularity is broken, it can cause errors and unexpected behavior in the code that uses the list.
Header Linked List:
A header linked list is a special type of linked list that contains a header node at the beginning of the list.
So, in a header linked list START will not point to the first node of the list but START will contain the address of the header node. Below is the image for Grounded Header Linked List:

Below is the Structure of the Grounded Header Linked List:
// Structure of the list
struct link {
int info;
// Pointer to the next node
struct link* next;
};
// C++ program to illustrate creation
// and traversal of Header Linked List
#include <bits/stdc++.h>
// Structure of the list
struct link {
int info;
struct link* next;
};
// Empty List
struct link* start = NULL;
// Function to create header of the
// header linked list
struct link* create_header_list(int data)
{
// Create a new node
struct link *new_node, *node;
new_node = (struct link*)malloc(sizeof(struct link));
new_node->info = data;
new_node->next = NULL;
// If it is the first node
if (start == NULL) {
// Initialize the start
start = (struct link*)malloc(sizeof(struct link));
start->next = new_node;
}
else {
// Insert the node in the end
node = start;
while (node->next != NULL) {
node = node->next;
}
node->next = new_node;
}
return start;
}
// Function to display the
// header linked list
struct link* display()
{
struct link* node;
node = start;
node = node->next;
// Traverse until node is
// not NULL
while (node != NULL) {
// Print the data
printf("%d ", node->info);
node = node->next;
}
printf("\n");
// Return the start pointer
return start;
}
// Driver Code
int main()
{
// Create the list
create_header_list(11);
create_header_list(12);
create_header_list(13);
// Print the list
printf("List After inserting"
" 3 elements:\n");
display();
create_header_list(14);
create_header_list(15);
// Print the list
printf("List After inserting"
" 2 more elements:\n");
display();
return 0;
}
Output
List After inserting 3 elements:
11 12 13
List After inserting 2 more elements:
11 12 13 14 15
Time Complexity:
The time complexity of creating a new node and inserting it at the end of the linked list is O(1).
The time complexity of traversing the linked list to display its contents is O(n), where n is the number of nodes in the list.
Therefore, the overall time complexity of creating and traversing a header linked list is O(n).
Applications of Header Linked List
The header linked lists are frequently used to maintain the polynomials in memory. The header node is used to represent the zero polynomial.
Suppose we have
F(x) = 5x5 – 3x3 + 2x2 + x1 +10x0From the polynomial represented by F(x) it is clear that this polynomial has two parts, coefficient and exponent, where, x is formal parameter. Hence, we can say that a polynomial is sum of terms, each of which consists of a coefficient and an exponent.
The computer implementation requires implementing polynomials as a list of pair of coefficient and exponent. Each of these pairs will constitute a structure, so a polynomial will be represented as a list of structures.
If one wants to represent F(x) with help of linked list then the list will contain 5 nodes. When we link each node we get a linked list structure that represents polynomial F(x).
Addition of polynomials
To add two polynomials, we need to scan them once.
If we find terms with the same exponent in the two polynomials, then we add the coefficients, otherwise, we copy the term of larger exponent into the sum and go on.
When we reach at the end of one of the polynomial, then remaining part of the other is copied into the sum.
Suppose we have two polynomials as illustrated and we have to perform addition of these polynomials.
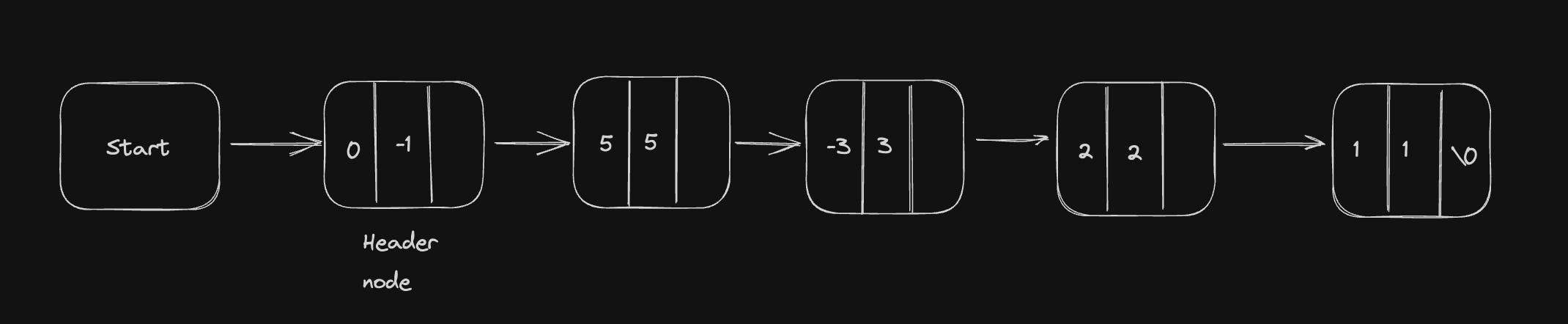
When we scan first node of the two polynomials, we find that exponential power of first node in the second polynomial is greater than that of first node of the first polynomial.
Here the exponent of the first node of the second polynomial is greater hence we have to copy first node of the second polynomial into the sum.
Then we consider the first node of the first polynomial and once again first node value of first polynomial is compared with the second node value of the second polynomial.
Here the first node exponent value of the first polynomial is greater than the second node exponent value of the second polynomial. We copy the first node of the first polynomial into the sum.
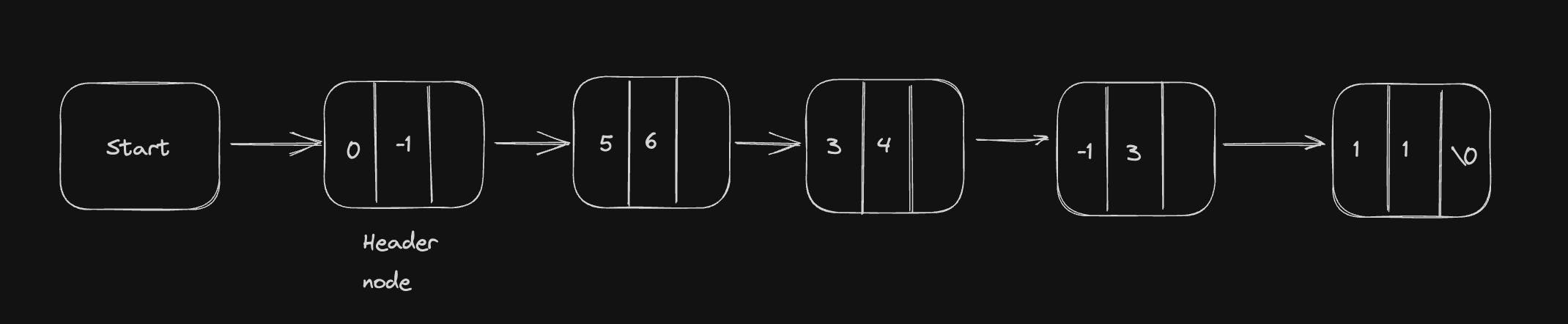
Now consider the second node of the first polynomial and compare it with the second node of the second polynomial.
Here the exponent value of the second node of the second polynomial is greater than the second node of the first polynomial, hence we copy the second node of the second list into the sum.
Now we consider the third node exponent of the second polynomial and compare it with second node exponent value of the first polynomial. We find that both are equal, hence perform addition of their coefficient and copy in to the sum.
This process continues till all the nodes of both the polynomial are exhausted. For example after adding the above two polynomials, we get the following resultant polynomial as shown.

That's all about Linked List I will further cover insertion and deletion into Linked List in my upcoming blogs. So make sure to subscribe me.
Some resources on Linked List for you all:
