Saving Memory Space: How to Handle Multiple Stacks with a Single Array

To store multiple stack in an array, the first approach that comes to your mind would be that you have an array of n elements and there are k stacks to be stored, and the first thing you will be doing is to make space for stacks that is you will divide the array into n/k stacks.

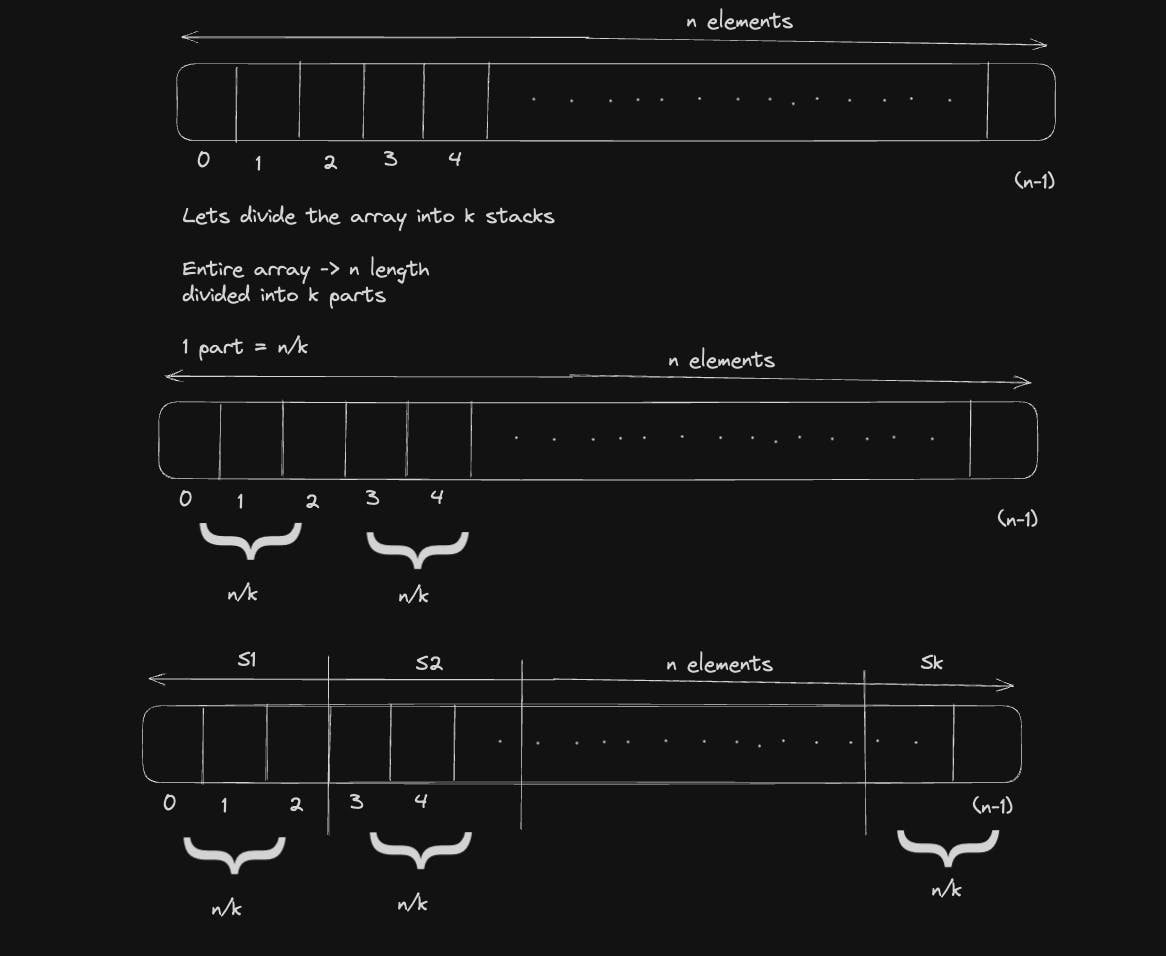
To perform push operation we will use push(x,m), where x is the value to be inserted and m is the stack number. Say if you have to push 5 in stack 2 that is S2, the push operation will be push(5,2) and to pop we will use pop(m).

But, there is a drawback in this approach, it is not space optimised. So, we will be looking at another approach.

Now, let us look at our second approach

Suppose that we have an array of 6 elements and we want to store 3 stacks in it. We will need two additional things, the first one is top[], which is an array that will store the position of the top elements of the stacks, its size will be the same as that of the number of stacks. And the other one is next[], it will point to the next element after stack top when stack is filled and it point to the next free space when stack is empty.

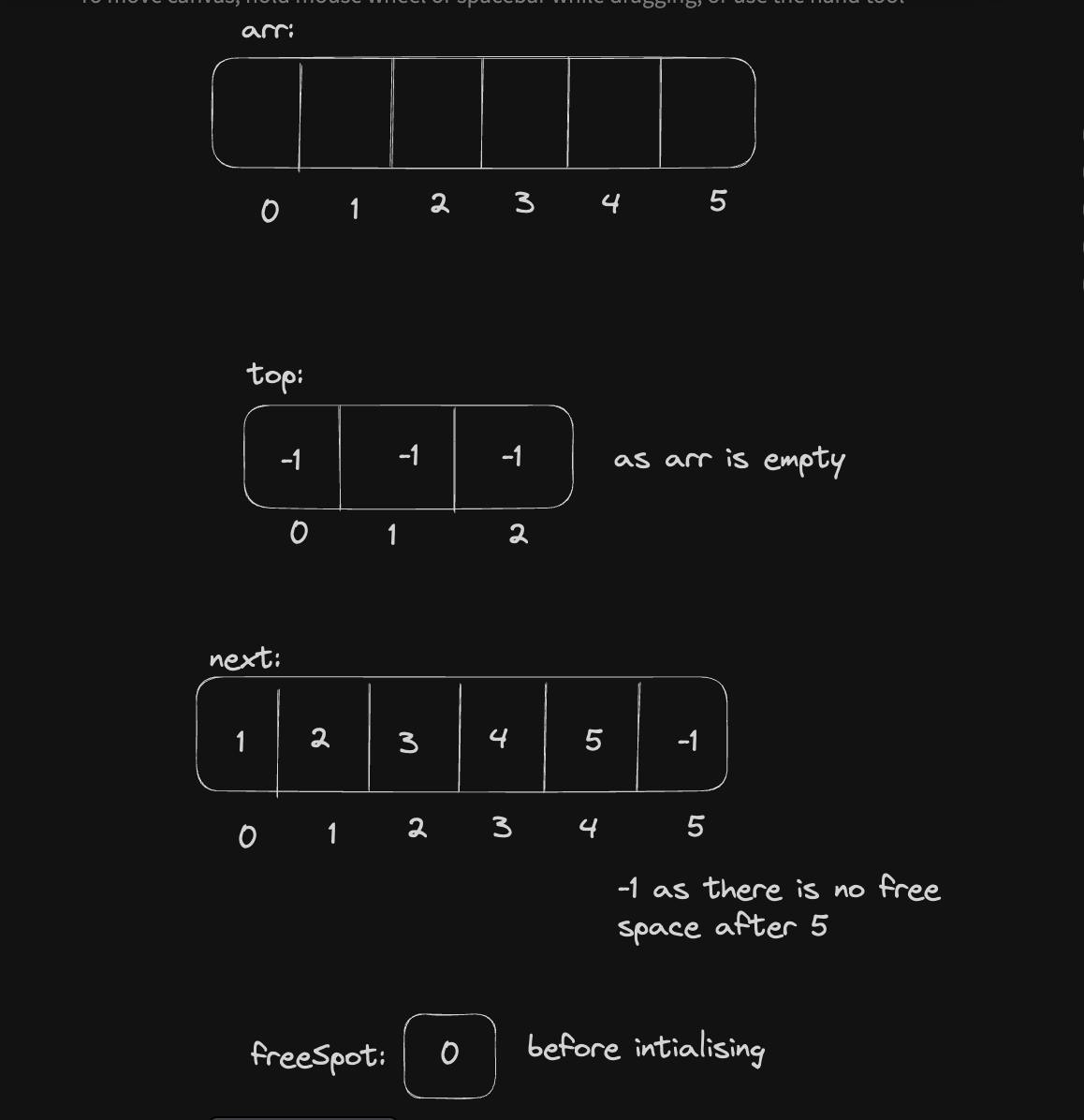
Now let us look at the algorithm to push an element:

push(10,1) -> this translates to push 10 in stack 1

1. Find index

   int index = freeSpot

2. update freeSpot

   freeSpot = next[index]

   freeSpot becomes 1 from 0

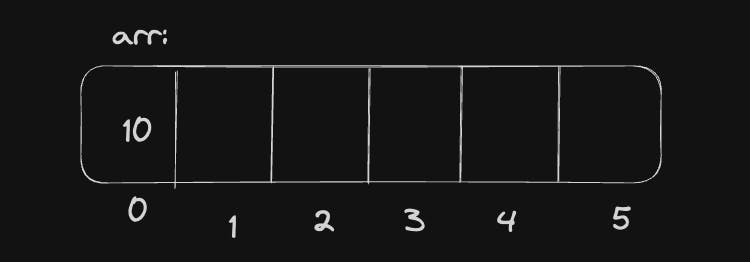
3. insert the element in array

   arr[index] = x

   

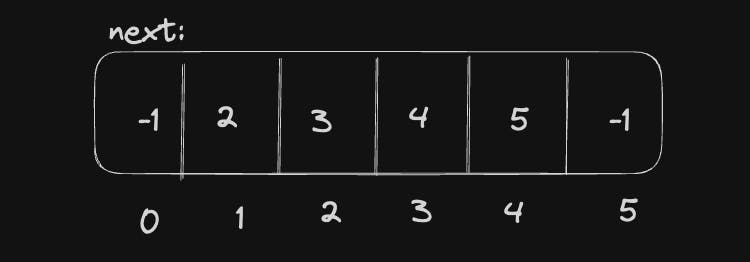
4. update next

   next[index] = top[m-1]

   

5. update top

   top[m-1] = index

The algorithm for pop operation is the reverse of the push.

// n stacks in an single array
#include <iostream>
using namespace std;

class Nstack
{
    int *arr;
    int *top;
    int *next;
    int n, s;
    int freeSpot;

public:
    Nstack(int N, int S)
    {
        n = N;
        s = S;
        arr = new int[s];
        top = new int[n];
        next = new int[s];

        // top initialise
        for (int i = 0; i < n; i++)
        {
            top[i] = -1;
        }

        // next initialise
        for (int i = 0; i < s; i++)
        {
            next[i] = i + 1;
        }

        // update last index value to -1
        next[s - 1] = -1;

        // initialise freeSpot
        freeSpot = 0;
    }
    // Pushes 'x' into the Mth stack. Returns true if get pushed
    bool push(int x, int m)
    {
        // Check for overflow
        if (freeSpot == -1)
        {
            return false;
        }

        // find index
        int index = freeSpot;

        // update freeSpot
        freeSpot = next[index];

        // insert element into array
        arr[index] = x;

        // update next
        next[index] = top[m - 1];

        // update top
        top[m - 1] = index;

        return true;
    }
    // Pops top element from Mth stack. Returns -1 if the stack is empty
    int pop(int m)
    {
        // check underflow
        if (top[m - 1] == -1)
        {
            return -1;
        }

        int index = top[m - 1];

        top[m - 1] = next[index];

        next[index] = freeSpot;

        freeSpot = index;

        return arr[index];
    }
};
int main()
{
    int numberOfStacks = 3;
    int SizeOfArray = 10;

    Nstack nStacks(numberOfStacks, SizeOfArray);

    // Push some elements into the first stack
    for (int i = 1; i <= 5; i++)
    {
        if (nStacks.push(i, 1))
        {
            cout << "Pushed " << i << " to Stack 1" << endl;
        }
        else
        {
            cout << "Stack 1 is full. Cannot push " << i << endl;
        }
    }

    // Push some elements into the second stack
    for (int i = 6; i <= 10; i++)
    {
        if (nStacks.push(i, 2))
        {
            cout << "Pushed " << i << " to Stack 2" << endl;
        }
        else
        {
            cout << "Stack 2 is full. Cannot push " << i << endl;
        }
    }

    // Push some elements into the third stack
    for (int i = 11; i <= 15; i++)
    {
        if (nStacks.push(i, 3))
        {
            cout << "Pushed " << i << " to Stack 3" << endl;
        }
        else
        {
            cout << "Stack 3 is full. Cannot push " << i << endl;
        }
    }

    // Pop elements from the first stack
    for (int i = 1; i <= 5; i++)
    {
        int value = nStacks.pop(1);
        if (value != -1)
        {
            cout << "Popped " << value << " from Stack 1" << endl;
        }
        else
        {
            cout << "Stack 1 is empty. Cannot pop." << endl;
        }
    }

    // Pop elements from the second stack
    for (int i = 1; i <= 5; i++)
    {
        int value = nStacks.pop(2);
        if (value != -1)
        {
            cout << "Popped " << value << " from Stack 2" << endl;
        }
        else
        {
            cout << "Stack 2 is empty. Cannot pop." << endl;
        }
    }

    // Pop elements from the third stack
    for (int i = 1; i <= 5; i++)
    {
        int value = nStacks.pop(3);
        if (value != -1)
        {
            cout << "Popped " << value << " from Stack 3" << endl;
        }
        else
        {
            cout << "Stack 3 is empty. Cannot pop." << endl;
        }
    }

    return 0;
}

output:
Pushed 1 to Stack 1
Pushed 2 to Stack 1
Pushed 3 to Stack 1
Pushed 4 to Stack 1
Pushed 5 to Stack 1
Pushed 6 to Stack 2
Pushed 7 to Stack 2
Pushed 8 to Stack 2
Pushed 9 to Stack 2
Pushed 11 to Stack 3
Stack 3 is full. Cannot push 12