Infix Notation

Infix is the day-to-day notation that we use of format A + B type. The general form can be classified as (a op b) where a and b are operands(variables) and op is the Operator.

• Example 1 : A + B

• Example 2 : A * B + C / D

Postfix Notation

Postfix is notation that the compiler uses/converts to while reading left to right and is of format AB+ type. The general form can be classified as (ab op) where a and b are operands(variables) and op is Operator.

• Example 1 : AB+

• Example 2 : AB*CD/+

Prefix Notation

Prefix is notation that the compiler uses/converts to while reading right to left (some compilers can also read prefix left to right) and is of format +AB type. The general form can be classified as (op ab) where a and b are operands(variables) and op is Operator.

• Example 1 : +AB

• Example 2 : +*AB/CD

Conversion of Infix expression to Postfix expression

1. Scan the infix expression from left to right.

2. If the scanned character is an operand, put it in the postfix expression.

3. Otherwise, do the following

   • If the precedence and associativity of the scanned operator are greater than the precedence and associativity of the operator in the stack [or the stack is empty or the stack contains a ‘(‘ ], then push it in the stack. [‘^‘ operator is right associative and other operators like ‘+‘,’–‘,’*‘ and ‘/‘ are left-associative].

     • Check especially for a condition when the operator at the top of the stack and the scanned operator both are ‘^‘. In this condition, the precedence of the scanned operator is higher due to its right associativity. So it will be pushed into the operator stack.

     • In all the other cases when the top of the operator stack is the same as the scanned operator, then pop the operator from the stack because of left associativity due to which the scanned operator has less precedence.

   • Else, Pop all the operators from the stack which are greater than or equal to in precedence than that of the scanned operator.

     • After doing that Push the scanned operator to the stack. (If you encounter parenthesis while popping then stop there and push the scanned operator in the stack.)

4. If the scanned character is a ‘(‘, push it to the stack.

5. If the scanned character is a ‘)’, pop the stack and output it until a ‘(‘ is encountered, and discard both the parenthesis.

6. Repeat steps 2-5 until the infix expression is scanned.

7. Once the scanning is over, Pop the stack and add the operators in the postfix expression until it is not empty.

8. Finally, print the postfix expression.

   For example:

   Consider the infix expression exp = “a+b*c+d”
   and the infix expression is scanned using the iterator i, which is initialized as i = 0.

   1st Step: Here i = 0 and exp[i] = ‘a’ i.e., an operand. So add this in the postfix expression. Therefore, postfix = “a”.

   

   Add ‘a’ in the postfix

   2nd Step: Here i = 1 and exp[i] = ‘+’ i.e., an operator. Push this into the stack. postfix = “a” and stack = {+}.

   

   Push ‘+’ in the stack

   3rd Step: Now i = 2 and exp[i] = ‘b’ i.e., an operand. So add this in the postfix expression. postfix = “ab” and stack = {+}.

   

   Add ‘b’ in the postfix

   4th Step: Now i = 3 and exp[i] = ‘*’ i.e., an operator. Push this into the stack. postfix = “ab” and stack = {+, *}.

   

   Push ‘*’ in the stack

   5th Step: Now i = 4 and exp[i] = ‘c’ i.e., an operand. Add this in the postfix expression. postfix = “abc” and stack = {+, *}.

   

   Add ‘c’ in the postfix

   6th Step: Now i = 5 and exp[i] = ‘+’ i.e., an operator. The topmost element of the stack has higher precedence. So pop until the stack becomes empty or the top element has less precedence. ‘*’ is popped and added in postfix. So postfix = “abc*” and stack = {+}.

   

   Pop ‘*’ and add in postfix

   Now the top element is ‘+‘which also same precedence. Pop it. postfix = “abc*+”.

   

   Pop ‘+’ and add it in postfix

   Now the stack is empty. So push ‘+’ in the stack. stack = {+}.

   

   Push ‘+’ in the stack

   7th Step: Now i = 6 and exp[i] = ‘d’ i.e., an operand. Add this in the postfix expression. postfix = “abc*+d”.

   

   Add ‘d’ in the postfix

   Final Step: Now no element is left. So empty the stack and add it in the postfix expression. postfix = “abc*+d+”.

   

   Pop ‘+’ and add it in postfix

Now the implementation of this algorithm is shown below:

// C++ code to convert infix expression to postfix

#include <iostream>
#include <stack>

using namespace std;

// Function to return precedence of operators
int prec(char c)
{
    if (c == '^')
        return 3;
    else if (c == '/' || c == '*')
        return 2;
    else if (c == '+' || c == '-')
        return 1;
    else
        return -1;
}

// The main function to convert infix expression
// to postfix expression
void infixToPostfix(string s)
{

    stack<char> st;
    string result;

    for (int i = 0; i < s.length(); i++)
    {
        char c = s[i];

        // If the scanned character is
        // an operand, add it to output string.
        if ((c >= 'a' && c <= 'z') || (c >= 'A' && c <= 'Z') || (c >= '0' && c <= '9'))
            result += c;

        // If the scanned character is an
        // ‘(‘, push it to the stack.
        else if (c == '(')
            st.push('(');

        // If the scanned character is an ‘)’,
        // pop and add to output string from the stack
        // until an ‘(‘ is encountered.
        else if (c == ')')
        {
            while (st.top() != '(')
            {
                result += st.top();
                st.pop();
            }
            st.pop();
        }

        // If an operator is scanned
        else
        {
            while (!st.empty() && prec(s[i]) <= prec(st.top()))
            {
                result += st.top();
                st.pop();
            }
            st.push(c);
        }
    }

    // Pop all the remaining elements from the stack
    while (!st.empty())
    {
        result += st.top();
        st.pop();
    }

    cout << result << endl;
}

// Driver code
int main()
{
    string exp = "a+b*(c^d-e)^(f+g*h)-i";

    // Function call
    infixToPostfix(exp);

    return 0;
}
Output: abcd^e-fgh*+^*+i-

Conversion of infix expression to prefix expression

• Step 1: Reverse the infix expression. Note while reversing each ‘(‘ will become ‘)’ and each ‘)’ becomes ‘(‘.

• Step 2: Convert the reversed infix expression to postfix expression*.*

  • While converting to postfix expression, instead of using pop operation to pop operators with greater than or equal precedence, here we will only pop the operators from stack that have greater precedence.

• Step 3: Reverse the postfix expression.

The stack is used to convert infix expression to postfix form.

Illustration:

See the below image for a clear idea:

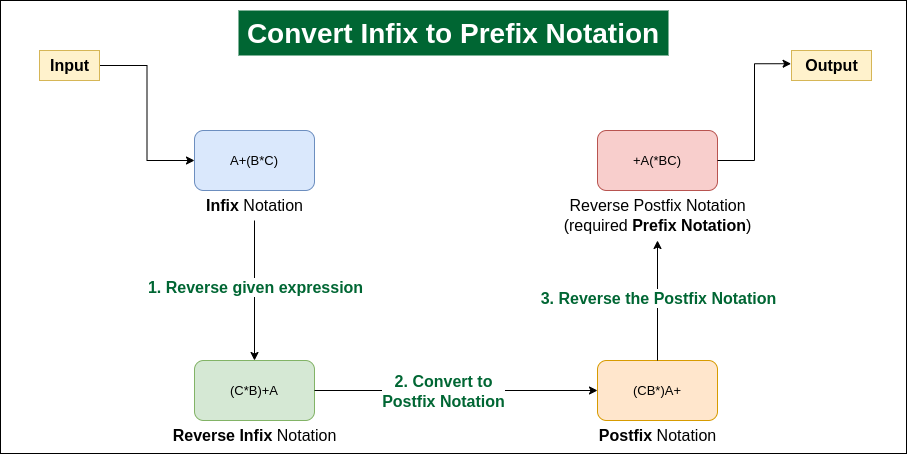
Convert infix expression to prefix expression

Below is the C++ implementation of the algorithm.

// C++ program to convert infix to prefix
#include <iostream>
#include <stack>

using namespace std;

// Function to check if the character is an operator
bool isOperator(char c)
{
    return (!isalpha(c) && !isdigit(c));
}

// Function to get the priority of operators
int getPriority(char C)
{
    if (C == '-' || C == '+')
        return 1;
    else if (C == '*' || C == '/')
        return 2;
    else if (C == '^')
        return 3;
    return 0;
}

// Function to convert the infix expression to postfix
string infixToPostfix(string infix)
{
    infix = '(' + infix + ')';
    int l = infix.size();
    stack<char> char_stack;
    string output;

    for (int i = 0; i < l; i++) {

        // If the scanned character is an
        // operand, add it to output.
        if (isalpha(infix[i]) || isdigit(infix[i]))
            output += infix[i];

        // If the scanned character is an
        // ‘(‘, push it to the stack.
        else if (infix[i] == '(')
            char_stack.push('(');

        // If the scanned character is an
        // ‘)’, pop and output from the stack
        // until an ‘(‘ is encountered.
        else if (infix[i] == ')') {
            while (char_stack.top() != '(') {
                output += char_stack.top();
                char_stack.pop();
            }

            // Remove '(' from the stack
            char_stack.pop();
        }

        // Operator found
        else {
            if (isOperator(char_stack.top())) {
                if (infix[i] == '^') {
                    while (
                        getPriority(infix[i])
                        <= getPriority(char_stack.top())) {
                        output += char_stack.top();
                        char_stack.pop();
                    }
                }
                else {
                    while (
                        getPriority(infix[i])
                        < getPriority(char_stack.top())) {
                        output += char_stack.top();
                        char_stack.pop();
                    }
                }

                // Push current Operator on stack
                char_stack.push(infix[i]);
            }
        }
    }
    while (!char_stack.empty()) {
        output += char_stack.top();
        char_stack.pop();
    }
    return output;
}

// Function to convert infix to prefix notation
string infixToPrefix(string infix)
{
    // Reverse String and replace ( with ) and vice versa
    // Get Postfix
    // Reverse Postfix
    int l = infix.size();

    // Reverse infix
    reverse(infix.begin(), infix.end());

    // Replace ( with ) and vice versa
    for (int i = 0; i < l; i++) {

        if (infix[i] == '(') {
            infix[i] = ')';
        }
        else if (infix[i] == ')') {
            infix[i] = '(';
        }
    }

    string prefix = infixToPostfix(infix);

    // Reverse postfix
    reverse(prefix.begin(), prefix.end());

    return prefix;
}

// Driver code
int main()
{
    string s = ("x+y*z/w+u");

    // Function call
    cout << infixToPrefix(s) << std::endl;
    return 0;
}

Output: ++x/*yzwu

Conversion of Postfix expression to Infix expression

We have already discussed Infix to Postfix. Below is an algorithm for Postfix to Infix.

Algorithm
Create an empty stack to store operands.

1. Iterate through each symbol in the postfix expression from left to right.

   a. If the symbol is an operand (e.g., a number or a variable):

   i. Push it onto the stack as a string.

   b. If the symbol is an operator:

   i. Pop the top two values from the stack as strings, let's call them operand1 and operand2.

   ii. Create a new string result by concatenating operand1, the operator symbol, and operand2 within parentheses.

   iii. Push the result string back onto the stack.

2. After processing all symbols in the postfix expression, the stack should contain a single string, which represents the infix expression.

3. Pop the string from the stack, and it is your final infix expression.

Here's a C++ implementation based on this algorithm:

// CPP program to find infix for
// a given postfix.

#include <iostream>
#include <stack>

using namespace std;

bool isOperand(char x)
{
return (x >= 'a' && x <= 'z') ||
        (x >= 'A' && x <= 'Z');
}

// Get Infix for a given postfix
// expression
string getInfix(string exp)
{
    stack<string> s;

    for (int i=0; exp[i]!='\0'; i++)
    {
        // Push operands
        if (isOperand(exp[i]))
        {
        string op(1, exp[i]);
        s.push(op);
        }

        // We assume that input is
        // a valid postfix and expect
        // an operator.
        else
        {
            string op1 = s.top();
            s.pop();
            string op2 = s.top();
            s.pop();
            s.push("(" + op2 + exp[i] +
                op1 + ")");
        }
    }

    // There must be a single element
    // in stack now which is the required
    // infix.
    return s.top();
}

// Driver code
int main()
{
    string exp = "ab*c+";
    cout << getInfix(exp);
    return 0;
}

Output: ((a*b)+c)

Conversion of Postfix expression to Prefix expression

Algorithm for Postfix to Prefix:

• Read the Postfix expression from left to right

• If the symbol is an operand, then push it onto the Stack

• If the symbol is an operator, then pop two operands from the Stack
  Create a string by concatenating the two operands and the operator before them. string = operator + operand2 + operand1 And push the resultant string back to Stack

• Repeat the above steps until end of Postfix expression.

// CPP Program to convert postfix to prefix

#include <iostream>
#include <stack>
using namespace std;

// function to check if character is operator or not
bool isOperator(char x)
{
    switch (x) {
    case '+':
    case '-':
    case '/':
    case '*':
        return true;
    }
    return false;
}

// Convert postfix to Prefix expression
string postToPre(string post_exp)
{
    stack<string> s;

    // length of expression
    int length = post_exp.size();

    // reading from left to right
    for (int i = 0; i < length; i++) {

        // check if symbol is operator
        if (isOperator(post_exp[i])) {

            // pop two operands from stack
            string op1 = s.top();
            s.pop();
            string op2 = s.top();
            s.pop();

            // concat the operands and operator
            string temp = post_exp[i] + op2 + op1;

            // Push string temp back to stack
            s.push(temp);
        }

        // if symbol is an operand
        else {

            // push the operand to the stack
            s.push(string(1, post_exp[i]));
        }
    }

    string ans = "";
    while (!s.empty()) {
        ans += s.top();
        s.pop();
    }
    return ans;
}

// Driver Code
int main()
{
    string post_exp = "ABC/-AK/L-*";

    // Function call
    cout << "Prefix : " << postToPre(post_exp);
    return 0;
}

Output: Prefix : *-A/BC-/AKL

Conversion of Prefix expression to Infix expression

Algorithm for Prefix to Infix:

• Read the Prefix expression in reverse order (from right to left)

• If the symbol is an operand, then push it onto the Stack

• If the symbol is an operator, then pop two operands from the Stack
  Create a string by concatenating the two operands and the operator between them.
  string = (operand1 + operator + operand2)
  And push the resultant string back to Stack

• Repeat the above steps until the end of Prefix expression.

• At the end, stack will have only 1 string i.e. resultant string

// C++ Program to convert prefix to Infix
#include <iostream>
#include <stack>
using namespace std;

// function to check if character is operator or not
bool isOperator(char x) {
switch (x) {
case '+':
case '-':
case '/':
case '*':
case '^':
case '%':
    return true;
}
return false;
}

// Convert prefix to Infix expression
string preToInfix(string pre_exp) {
stack<string> s;

// length of expression
int length = pre_exp.size();

// reading from right to left
for (int i = length - 1; i >= 0; i--) {

    // check if symbol is operator
    if (isOperator(pre_exp[i])) {

    // pop two operands from stack
    string op1 = s.top(); s.pop();
    string op2 = s.top(); s.pop();

    // concat the operands and operator
    string temp = "(" + op1 + pre_exp[i] + op2 + ")";

    // Push string temp back to stack
    s.push(temp);
    }

    // if symbol is an operand
    else {

    // push the operand to the stack
    s.push(string(1, pre_exp[i]));
    }
}

// Stack now contains the Infix expression
return s.top();
}

// Driver Code
int main() {
string pre_exp = "*-A/BC-/AKL";
cout << "Infix : " << preToInfix(pre_exp);
return 0;
}

Output: Infix : ((A-(B/C))*((A/K)-L))

Conversion of Prefix expression to Posfix expression

Algorithm for Prefix to Postfix:

• Read the Prefix expression in reverse order (from right to left)

• If the symbol is an operand, then push it onto the Stack

• If the symbol is an operator, then pop two operands from the Stack
  Create a string by concatenating the two operands and the operator after them.
  string = operand1 + operand2 + operator
  And push the resultant string back to Stack

• Repeat the above steps until end of Prefix expression.

// CPP Program to convert prefix to postfix
#include <iostream>
#include <stack>
using namespace std;

// function to check if character is operator or not
bool isOperator(char x)
{
    switch (x) {
    case '+':
    case '-':
    case '/':
    case '*':
        return true;
    }
    return false;
}

// Convert prefix to Postfix expression
string preToPost(string pre_exp)
{

    stack<string> s;
    // length of expression
    int length = pre_exp.size();

    // reading from right to left
    for (int i = length - 1; i >= 0; i--)
    {
        // check if symbol is operator
        if (isOperator(pre_exp[i]))
        {
            // pop two operands from stack
            string op1 = s.top();
            s.pop();
            string op2 = s.top();
            s.pop();

            // concat the operands and operator
            string temp = op1 + op2 + pre_exp[i];

            // Push string temp back to stack
            s.push(temp);
        }

        // if symbol is an operand
        else {

            // push the operand to the stack
            s.push(string(1, pre_exp[i]));
        }
    }

    // stack contains only the Postfix expression
    return s.top();
}

// Driver Code
int main()
{
    string pre_exp = "*-A/BC-/AKL";
    cout << "Postfix : " << preToPost(pre_exp);
    return 0;
}

Output: Postfix : ABC/-AK/L-*

The provided information explains various notations for representing mathematical expressions, such as infix, postfix, and prefix notations. It also presents algorithms and code implementations for converting expressions between these notations in the context of a programming language like C++.

Infix Notation:

• Infix notation is the common mathematical notation we use daily, like A + B.

• The general form is (a op b), where a and b are operands, and op is an operator.

Postfix Notation (Reverse Polish Notation, RPN):

• Postfix notation is used by compilers while reading from left to right, e.g., AB+.

• The general form is (ab op), where a and b are operands, and op is an operator.

Prefix Notation (Polish Notation):

• Prefix notation is used by some compilers while reading from right to left or left to right, e.g., +AB.

• The general form is (op ab), where a and b are operands, and op is an operator.

Conversion from Infix to Postfix:

• Scan the infix expression from left to right.

• Use a stack to manage operators.

• Apply operator precedence and associativity rules.

• Convert to postfix notation, which is more suitable for evaluation.

Conversion from Infix to Prefix:

• Reverse the infix expression and switch '(' and ')' symbols.

• Convert to postfix notation.

• Reverse the postfix expression to obtain the prefix notation.

Conversion from Postfix to Infix:

• Use a stack to manage operands and operators.

• Iterate through the postfix expression, combining operands and operators to form an infix expression.

Conversion from Prefix to Infix:

• Use a stack to manage operands and operators.

• Iterate through the prefix expression (in reverse), combining operands and operators to form an infix expression.

Conversion from Prefix to Postfix:

• Use a stack to manage operands and operators.

• Iterate through the prefix expression (in reverse), combining operands and operators to form a postfix expression.

Code Implementations:

• C++ code examples are provided for each conversion operation.

• The code uses stacks to manage operators and operands.

• The algorithms handle operator precedence and associativity rules.

• They convert expressions between infix, postfix, and prefix notations based on the specified rules.

These algorithms and code implementations are useful in various programming and compiler-related tasks, especially for handling mathematical expressions in different notations.